In this experiment, we get to understand how does potential wells work for particle, and the wells act like a box so the particle can have behavior similar to standing waves.
1. From your study of mechanical waves, what is the longest wavelength standing wave on a string of length L?
A1: The longest wavelength you can get is when n=1, which is the fundamental frequency
Question 2: The de Broglie Relation
What is the momentum of the longest wavelength standing wave in a box of length L?
A2: p=h/2L where 2L is the wavelength, and h is Planck's constant
Question 3: Ground State Energy
Assuming the particle is not traveling at relativistic speeds, determine an expression for the ground state energy.
A3: E=h^2/(8mL) where m is the mass of the particle
Question 4: Increasing L
If the size of the box is increased, will the ground state energy increase or decrease?
A4: According to the equation from the previous question, the energy will decrease when the size of the box increased
Question 5: The Correspondence Principle: Large Size
In the limit of a very large box, what will happen to the ground state energy and the spacing between allowed energy levels? Can this result explain why quantum effects are not noticable in everyday, macroscopic situations?
A5: When the size of the large box, the energy difference with two states become smaller
Question 6: The Correspondence Principle: Large Mass
In the limit of a very massive particle, what will happen to the ground state energy and the spacing between allowed energy levels?
A6: According to the formula, when the mass increase, the energy difference of two states become smaller
Question 7: Ground State Probability
If a measurement is made of the particle's position while in the ground state, at what position is it most likely to be detected?
A7: When you take the wave function square to find the probability, the particle is most likely to find in the middle of the box
Question 8: Probability: Dependence on Mass and Size
The most likely position to detect the particle, when it is in the ground state, is in the center of the box. Does this observation depend on either the mass of the particle or the size of the box?
A8: It does not depend on neither the mass nor the size of the box
Question 9: Probability: Dependence on Energy Level
The most likely position to detect the particle, when it is in the ground state, is in the center of the box. Does this observation hold true at higher energy levels?
A9: When you look at the wave function, if we use schrodinger's equation, the energy is not the highest in th center of the box
Question 10: The Correspondence Principle: Large n
In the limit of large n, what will happen to the spacing between regions of high and low probability of detection? Does this agree with what is observed in everyday, macroscopic situations?
A10: When we have a large n value, the particle acts like a free particle; thus, the probability to find the particle can be describe as zero
Tuesday, December 13, 2011
Tuesday, December 6, 2011
Planck's Constant from an LED*
The purpose of the experiment is to determine the Planck's Constant with different color of LEDs
LED stands for Light Emitting Diode. We also learned the basic concept of diode during the lecture.
In this experiment, we have four different color of LED's, which are red, green, yellow, and blue.
We use the same setup as we did in the gas spectra experience to determine the wave length of the light that is emitted from the diode.
Also, we measured the voltage drop across the diode to determine the power input of the LED.
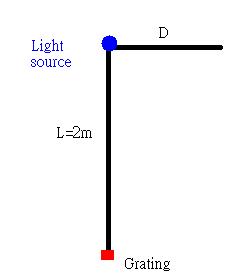
We have a distance of 2m between the light source and the grating. The good thing about the grating we had is that it has a label on the side; thus, we also knew what is the grating size.
the equation we got to determine the wavelength is lambda=Dd/(sqrt(L^2+D^2)) where D is the distance of the spectra light and d is the grating size. L is the distance between the light source and the grating.
We use the same set up
LED stands for Light Emitting Diode. We also learned the basic concept of diode during the lecture.
In this experiment, we have four different color of LED's, which are red, green, yellow, and blue.
We use the same setup as we did in the gas spectra experience to determine the wave length of the light that is emitted from the diode.
Also, we measured the voltage drop across the diode to determine the power input of the LED.
We have a distance of 2m between the light source and the grating. The good thing about the grating we had is that it has a label on the side; thus, we also knew what is the grating size.
the equation we got to determine the wavelength is lambda=Dd/(sqrt(L^2+D^2)) where D is the distance of the spectra light and d is the grating size. L is the distance between the light source and the grating.
We use the same set up
But with the different numbers
d(m) | 1.67E-06 |
L(m) | 1.29 |
Ω | 680 |
LED | D(m) | Uncertain(cm) | Upper | Lower |
Red | 0.54 | 0.01 | 0.55 | 0.53 |
Green | 0.42 | 0.01 | 0.43 | 0.41 |
Blue | 0.38 | 0.01 | 0.39 | 0.37 |
Yellow | 0.49 | 0.01 | 0.5 | 0.48 |
LED | λ(m) | Uncertain(m) | Upper(m) | Lower(m) |
Red | 6.449E-07 | 1.016E-08 | 6.550E-07 | 6.346E-07 |
Green | 5.170E-07 | 1.113E-08 | 5.281E-07 | 5.058E-07 |
Blue | 4.719E-07 | 1.143E-08 | 4.833E-07 | 4.604E-07 |
Yellow | 5.930E-07 | 1.058E-08 | 6.035E-07 | 5.824E-07 |
LED | Voltage drop(v) | 1/λ(m-1) | Uncertain(v) | Upper | Lower |
Red | 1.86 | 1.551E+06 | 0.005 | 1.865 | 1.855 |
Green | 2.50 | 1.934E+06 | 0.005 | 2.505 | 2.495 |
Blue | 2.66 | 2.119E+06 | 0.005 | 2.665 | 2.655 |
Yellow | 1.90 | 1.686E+06 | 0.005 | 1.905 | 1.895 |
If we graph V vs. 1/Wavelength
we will get
The slope value we get is 1.573E-6 v*m. If we multiply q and divide speed of light we should get the value of Planck's constant which is 8.756E-34 J*s. The percent error of our result is about 33%. But we have a large range of uncertainties for all the variables and a significant amount from the small angle approximation. Thus, we can conclude that our experiment has succeed to measure Planck's Constant
The Red LED consumed the least amount energy and the Blue LED consumed the most. This reason is that Red has a longer wavelength (lower energy) but Blue has a shorter wavelength(higher energy) according to the equation
E=hc/λ where h is the planck's constant, c is speed of light, and λ is the wavelength.
Subscribe to:
Comments (Atom)