In this experiment, we get to understand how does potential wells work for particle, and the wells act like a box so the particle can have behavior similar to standing waves.
1. From your study of mechanical waves, what is the longest wavelength standing wave on a string of length L?
A1: The longest wavelength you can get is when n=1, which is the fundamental frequency
Question 2: The de Broglie Relation
What is the momentum of the longest wavelength standing wave in a box of length L?
A2: p=h/2L where 2L is the wavelength, and h is Planck's constant
Question 3: Ground State Energy
Assuming the particle is not traveling at relativistic speeds, determine an expression for the ground state energy.
A3: E=h^2/(8mL) where m is the mass of the particle
Question 4: Increasing L
If the size of the box is increased, will the ground state energy increase or decrease?
A4: According to the equation from the previous question, the energy will decrease when the size of the box increased
Question 5: The Correspondence Principle: Large Size
In the limit of a very large box, what will happen to the ground state energy and the spacing between allowed energy levels? Can this result explain why quantum effects are not noticable in everyday, macroscopic situations?
A5: When the size of the large box, the energy difference with two states become smaller
Question 6: The Correspondence Principle: Large Mass
In the limit of a very massive particle, what will happen to the ground state energy and the spacing between allowed energy levels?
A6: According to the formula, when the mass increase, the energy difference of two states become smaller
Question 7: Ground State Probability
If a measurement is made of the particle's position while in the ground state, at what position is it most likely to be detected?
A7: When you take the wave function square to find the probability, the particle is most likely to find in the middle of the box
Question 8: Probability: Dependence on Mass and Size
The most likely position to detect the particle, when it is in the ground state, is in the center of the box. Does this observation depend on either the mass of the particle or the size of the box?
A8: It does not depend on neither the mass nor the size of the box
Question 9: Probability: Dependence on Energy Level
The most likely position to detect the particle, when it is in the ground state, is in the center of the box. Does this observation hold true at higher energy levels?
A9: When you look at the wave function, if we use schrodinger's equation, the energy is not the highest in th center of the box
Question 10: The Correspondence Principle: Large n
In the limit of large n, what will happen to the spacing between regions of high and low probability of detection? Does this agree with what is observed in everyday, macroscopic situations?
A10: When we have a large n value, the particle acts like a free particle; thus, the probability to find the particle can be describe as zero
Tuesday, December 13, 2011
Tuesday, December 6, 2011
Planck's Constant from an LED*
The purpose of the experiment is to determine the Planck's Constant with different color of LEDs
LED stands for Light Emitting Diode. We also learned the basic concept of diode during the lecture.
In this experiment, we have four different color of LED's, which are red, green, yellow, and blue.
We use the same setup as we did in the gas spectra experience to determine the wave length of the light that is emitted from the diode.
Also, we measured the voltage drop across the diode to determine the power input of the LED.
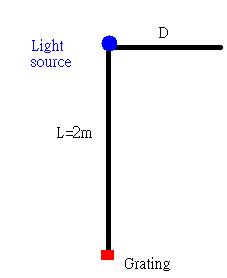
We have a distance of 2m between the light source and the grating. The good thing about the grating we had is that it has a label on the side; thus, we also knew what is the grating size.
the equation we got to determine the wavelength is lambda=Dd/(sqrt(L^2+D^2)) where D is the distance of the spectra light and d is the grating size. L is the distance between the light source and the grating.
We use the same set up
LED stands for Light Emitting Diode. We also learned the basic concept of diode during the lecture.
In this experiment, we have four different color of LED's, which are red, green, yellow, and blue.
We use the same setup as we did in the gas spectra experience to determine the wave length of the light that is emitted from the diode.
Also, we measured the voltage drop across the diode to determine the power input of the LED.
We have a distance of 2m between the light source and the grating. The good thing about the grating we had is that it has a label on the side; thus, we also knew what is the grating size.
the equation we got to determine the wavelength is lambda=Dd/(sqrt(L^2+D^2)) where D is the distance of the spectra light and d is the grating size. L is the distance between the light source and the grating.
We use the same set up
But with the different numbers
d(m) | 1.67E-06 |
L(m) | 1.29 |
Ω | 680 |
LED | D(m) | Uncertain(cm) | Upper | Lower |
Red | 0.54 | 0.01 | 0.55 | 0.53 |
Green | 0.42 | 0.01 | 0.43 | 0.41 |
Blue | 0.38 | 0.01 | 0.39 | 0.37 |
Yellow | 0.49 | 0.01 | 0.5 | 0.48 |
LED | λ(m) | Uncertain(m) | Upper(m) | Lower(m) |
Red | 6.449E-07 | 1.016E-08 | 6.550E-07 | 6.346E-07 |
Green | 5.170E-07 | 1.113E-08 | 5.281E-07 | 5.058E-07 |
Blue | 4.719E-07 | 1.143E-08 | 4.833E-07 | 4.604E-07 |
Yellow | 5.930E-07 | 1.058E-08 | 6.035E-07 | 5.824E-07 |
LED | Voltage drop(v) | 1/λ(m-1) | Uncertain(v) | Upper | Lower |
Red | 1.86 | 1.551E+06 | 0.005 | 1.865 | 1.855 |
Green | 2.50 | 1.934E+06 | 0.005 | 2.505 | 2.495 |
Blue | 2.66 | 2.119E+06 | 0.005 | 2.665 | 2.655 |
Yellow | 1.90 | 1.686E+06 | 0.005 | 1.905 | 1.895 |
If we graph V vs. 1/Wavelength
we will get
The slope value we get is 1.573E-6 v*m. If we multiply q and divide speed of light we should get the value of Planck's constant which is 8.756E-34 J*s. The percent error of our result is about 33%. But we have a large range of uncertainties for all the variables and a significant amount from the small angle approximation. Thus, we can conclude that our experiment has succeed to measure Planck's Constant
The Red LED consumed the least amount energy and the Blue LED consumed the most. This reason is that Red has a longer wavelength (lower energy) but Blue has a shorter wavelength(higher energy) according to the equation
E=hc/λ where h is the planck's constant, c is speed of light, and λ is the wavelength.
Tuesday, November 15, 2011
Color And Spectra
There are three parts with this experiment. The first part is to look at the light spectra of white light through a grating. The second part is to look at an unknown gas to with a grating to determine the contents of the tube with spectra lines. Last, we compare the wavelength results to fix any systematic shift with an equation. After, we determine the possible wave lengths of the hydrogen gas tube.
For the following experiment, the apparatus is
The value of the grating will be 1.67*10^-6 m
The equation to find the wavelength at distinct position is λ=(D*d)/√(L^2+D^2) where D is the spectra light's distance from the light source. L is the distance between the light source and the grating. d is the measurment of the grating.
We just look through the grating to determine the spectra lines.
1.
For experiment one, the light source will be white light (regular light bulb), and we measured the distance for the spectra light. Interesting thing about this experiment is that the light bulb has some diameter about 1.5cm;thus, we need to add this number to compensate the increase in the value of L(2.015m). By doing the experience we obtained the value of each spectra line (the midpoint of continuous spectra)
End points are 42cm &85.5cm
If we look only at the end points of the spectra lines, we range of the wavelength is gonna be 341nm~652nm±10nm
The results we got from doing the experiment is within the visible spectra, which is 380~750nm(according to wikipedia).
2. The second experiment is to determine the type of gas inside the tube we have
In this case, we do the same steps with just the white light to determine the spectra line ragnes are.
If we take the the midpoint of each region we get
Violet=52.25cm±0.25cm
Green=60.75cm±0.25cm
Yello=64.5cm±0.25cm
Red=66.5cm±0.25cm
If we calculated out the wavelength of each section
we get
Violet=422nm±4nm
Green=485nm+4nm
Yellow=513nm±4nm
Red=642nm+±4nm
If we match the spectra line we have to an known gas spectra, we will get the result similar to mercury gas.
3. Lastly, we use the same method the measure the four primary lines of the hydrogen gas spectrum.
The problem we had for this experiment is that our hydrogen gas tube has a leak;thus, the light that produced is really dean that we had trouble to do this experiment. At the end, we just worked with Christ and Eric to do the experiment and obtained the data from them.
And to fixed the systematic error they had the equation of λ_actual=1.051λ_exp+4.538
If we calculate the numbers, we will get
Violet/Blue=378nm±11nm
Green=410nm±11nm
Orange/Yello=495nm±11nm
Red=557nm±11nm
After the calibration, the actual result is
Violet/Blue=402nm±16nm
Green=435nm±16nm
Orange/Yello=525nm±16nm
Red=590nm±16nm
And if we compare to the actual results
The results are fairly close to the actual number within their uncertainties.
For the following experiment, the apparatus is
The value of the grating will be 1.67*10^-6 m
The equation to find the wavelength at distinct position is λ=(D*d)/√(L^2+D^2) where D is the spectra light's distance from the light source. L is the distance between the light source and the grating. d is the measurment of the grating.
We just look through the grating to determine the spectra lines.
1.
For experiment one, the light source will be white light (regular light bulb), and we measured the distance for the spectra light. Interesting thing about this experiment is that the light bulb has some diameter about 1.5cm;thus, we need to add this number to compensate the increase in the value of L(2.015m). By doing the experience we obtained the value of each spectra line (the midpoint of continuous spectra)
Violet | Blue | Green | Yellow | Red | |
cm+-0.5cm | 43.5 | 49.5 | 58.5 | 65 | 76 |
If we look only at the end points of the spectra lines, we range of the wavelength is gonna be 341nm~652nm±10nm
The results we got from doing the experiment is within the visible spectra, which is 380~750nm(according to wikipedia).
In this case, we do the same steps with just the white light to determine the spectra line ragnes are.
Violet | Green | Yellow | Red | |
cm+-0.5cm | 45.5~59 | 59~62.5 | 62.5~66.5 | 66.5~100 |
Violet=52.25cm±0.25cm
Green=60.75cm±0.25cm
Yello=64.5cm±0.25cm
Red=66.5cm±0.25cm
If we calculated out the wavelength of each section
we get
Violet=422nm±4nm
Green=485nm+4nm
Yellow=513nm±4nm
Red=642nm+±4nm
If we match the spectra line we have to an known gas spectra, we will get the result similar to mercury gas.
3. Lastly, we use the same method the measure the four primary lines of the hydrogen gas spectrum.
The problem we had for this experiment is that our hydrogen gas tube has a leak;thus, the light that produced is really dean that we had trouble to do this experiment. At the end, we just worked with Christ and Eric to do the experiment and obtained the data from them.
Violet/Blue | Green | Orange/Yellow | Red | |
cm+-2cm | 46.5 | 50.6 | 62.1 | 70.8 |
And to fixed the systematic error they had the equation of λ_actual=1.051λ_exp+4.538
If we calculate the numbers, we will get
Violet/Blue=378nm±11nm
Green=410nm±11nm
Orange/Yello=495nm±11nm
Red=557nm±11nm
After the calibration, the actual result is
Violet/Blue=402nm±16nm
Green=435nm±16nm
Orange/Yello=525nm±16nm
Red=590nm±16nm
And if we compare to the actual results
| Color | Frequency | Wavelength |
|---|---|---|
| violet | 668–789 THz | 380–450 nm |
| blue | 631–668 THz | 450–475 nm |
| cyan | 606–630 THz | 476–495 nm |
| green | 526–606 THz | 495–570 nm |
| yellow | 508–526 THz | 570–590 nm |
| orange | 484–508 THz | 590–620 nm |
| red | 400–484 THz | 620–750 nm |
The results are fairly close to the actual number within their uncertainties.
Visualizing Wave Packets
Today, we had our first computer lab experiment that we get to have the chance to play with python. Unlike in 4A, this time we use from pylab import* in-order to generate graphing ability to present in the program. The three parts of this program are: generate sin graph, generate Gaussian graph, and last is to generate multiple sin graph and add them together with different period and amplitude. The amplitude of
each graphs will depend on the Gaussian function.
In-order for the program to work, we need to install pylab library into our computer, we can obtain the file from the link http://sourceforge.ent/projects/matplotlib/
Here is the code we had
_________________________________below is the code_________________________________
from pylab import*
harmonics= 20
center=harmonics/2
sigma=1
coeff=1/((sqrt(2*pi))*sigma)
gauss_list=[]
domain_list2=[]
L=10
knot= 2*pi/L
b_list=[]
kdomain=[]
##
##for k in arange(0,200,0.1):
## bofk=(1/(knot))
## b_list.append(bofk)
## kdomain.append(k)
####plot(kdomain,b_list)
##
for x in range(1,harmonics):
gauss=coeff*exp(-(x-center)**2/(2.*sigma**2))
gauss_list.append(gauss)
domain_list2.append(x)
##A_coeff_1=1
##wave_constant_1=1
##sine1_list=[]
##domain_list=[]
##for x in arange(-pi,pi,0.1):
## sine1=A_coeff_1*sin(wave_constant_1*x)
## sine1_list.append(sine1)
## domain_list.append(x)
w=1
Fourier_Series=[]
for i in range(1,harmonics):
sine_function=[]
x=[]
for t in arange(-pi,pi,0.01):
sine_f=gauss_list[i-1]*sin(i*w*t)
sine_function.append(sine_f)
x.append(t)
##plot(x,sine_function)
Fourier_Series.append(sine_function)
superposition=zeros(len(sine_function))
for function in Fourier_Series:
for i in range(len(function)):
superposition[i]+=function[i]
print kdomain
plot(x,superposition)
##plot(domain_list2,gauss_list)
##plot(domain_list,sine1_list)
show()
_________________________________End of the code_________________________________
Here are some of the results that we got
First this is the graph for jut plotting one sine function
After this is to plot the Gaussian function
At the end, we combine the since function with amplitude of the results from Gaussian function
Also, if we put more sine function (harmonics), the tails of the graph will be longer
After computing these results, we were ask few questions
Using the integral in , determine the wave function
, determine the wave function  for a function
for a function  given by
given by
 .
.
This represents an equal combination of all wave numbers between 0 and . Thus
. Thus  represents a particle with average wave number
represents a particle with average wave number  , with a total spread or uncertainty in wave number of
, with a total spread or uncertainty in wave number of  . We will call this spread the width
. We will call this spread the width  of
of  , so
, so  .
.
a. Graph versus
versus  for the case
for the case  , where
, where  is a length.
is a length.
b. Graph versus
versus  for the case
for the case  , where
, where  is a length.
is a length.
c. Locate the two points closest to this maximum (one on each side of it) where , and define the distance along the
, and define the distance along the  -axis between these two points as
-axis between these two points as  , the width of
, the width of  . What is the value of
. What is the value of  if
if  ?
?
each graphs will depend on the Gaussian function.
In-order for the program to work, we need to install pylab library into our computer, we can obtain the file from the link http://sourceforge.ent/projects/matplotlib/
Here is the code we had
_________________________________below is the code_________________________________
from pylab import*
harmonics= 20
center=harmonics/2
sigma=1
coeff=1/((sqrt(2*pi))*sigma)
gauss_list=[]
domain_list2=[]
L=10
knot= 2*pi/L
b_list=[]
kdomain=[]
##
##for k in arange(0,200,0.1):
## bofk=(1/(knot))
## b_list.append(bofk)
## kdomain.append(k)
####plot(kdomain,b_list)
##
for x in range(1,harmonics):
gauss=coeff*exp(-(x-center)**2/(2.*sigma**2))
gauss_list.append(gauss)
domain_list2.append(x)
##A_coeff_1=1
##wave_constant_1=1
##sine1_list=[]
##domain_list=[]
##for x in arange(-pi,pi,0.1):
## sine1=A_coeff_1*sin(wave_constant_1*x)
## sine1_list.append(sine1)
## domain_list.append(x)
w=1
Fourier_Series=[]
for i in range(1,harmonics):
sine_function=[]
x=[]
for t in arange(-pi,pi,0.01):
sine_f=gauss_list[i-1]*sin(i*w*t)
sine_function.append(sine_f)
x.append(t)
##plot(x,sine_function)
Fourier_Series.append(sine_function)
superposition=zeros(len(sine_function))
for function in Fourier_Series:
for i in range(len(function)):
superposition[i]+=function[i]
print kdomain
plot(x,superposition)
##plot(domain_list2,gauss_list)
##plot(domain_list,sine1_list)
show()
_________________________________End of the code_________________________________
Here are some of the results that we got
First this is the graph for jut plotting one sine function
After this is to plot the Gaussian function
At the end, we combine the since function with amplitude of the results from Gaussian function
Also, if we put more sine function (harmonics), the tails of the graph will be longer
After computing these results, we were ask few questions
Using the integral in
This represents an equal combination of all wave numbers between 0 and
a. Graph
b. Graph
c. Locate the two points closest to this maximum (one on each side of it) where
A:  =1.00
=1.00 
d.Repeat part C for the case  .
.
e. Repeat part D for the case  .
.
f. The momentum  is equal to
is equal to  , so the width of
, so the width of  in momentum is
in momentum is  . Calculate the product
. Calculate the product  for the case
for the case 
A:  =
=
g. Calculate the product  for the case
for the case 
A:  =
=
h. Discuss your results in light of the Heisenberg uncertainty principle.
A: Since  =
= and according to Heisenber uncertainty, which is
and according to Heisenber uncertainty, which is  >=h/2π, the results is valid for any value of
>=h/2π, the results is valid for any value of 
Subscribe to:
Comments (Atom)